Permutations of a String - Unique Characters and Duplicates

$\mathtt{REFERENCE}$ @ Geek For Geeks

Permutation

Permutation of a set is simply a different ordering of the elements. For the given string, we can order the characters into different locations producing different string. All such strings constitute the permutation of that string.

Example: Permutation of a string XYZ are:

XYZ XZY YXZ YZX ZXY ZYX

For given string of length $n$ there are total of $n!$ permutations.

Algorithm - For String with Unique Characters

As explained HERE, following image explains how we can compute the permutations of given string.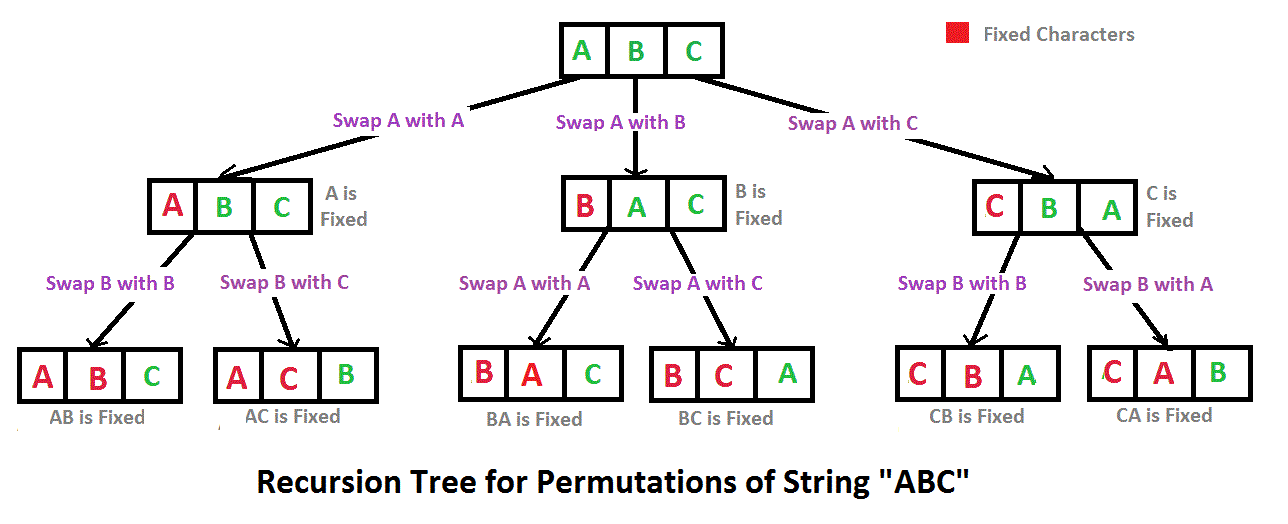

In this algorithm,

• For each character in the input String:
1. Select the character and keep it fixed.
2. Compute permutations of remaining $n-1$ characters.
3. Finally append all those permutations of $n-1$ characters to the character selected in the $Step\ 1$.

Algorithm - For String with Duplicate Characters

Algorithms described above will also work with strings with duplicate characters. However, the algorithm will also produce duplicate results. So a simple solution will be to check for unique solutions, probably using Hashing, in the above solution.

Problem

The problem with this solution is, for a string with two many duplicate characters, it will end up computing all $n!$ solutions while there are very few number of solutions.

Example: String AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA has only one permutation which the input string itself.

But the above algorithm will be doing a lot of unnecessary computation.

Solution

So for string with duplicate entries, we can write efficient solution. For string with all unique characters, its performance will still become $n!$.

The solution is very much similar to the Coin Exchange Problem.

In this algorithm,

1. We can create Frequency table which keeps count of all unique characters in the string.
2. For each unique character if it count is Greater Than 0:
   1. Append the character to Current Permutation. When length of the Current Permutation is equal to the length of input string, we have one solution.
   2. Decrease count by 1.
   3. Recurse through the same updated Map.
   4. Reset or Increase the count by 1.

Implementation (Both Method)

Following is the implementation for both the method.

Time Complexity

There are $n!$ permutations. We need to compute each of these permutations. $\therefore$ The complexity of this approach is $\cal{\theta(n!)}$ which is exponential with the size of the input.

---

---

---