Detect Loop in Linked List And Identify the Start of Loop

Task Description

Detect if a given linked list has a loop. If it has a loop, find the starting node of the loop.

Solution 1 : Simple Solution

When I first came across this problem, the solution that I thought of was to traverse through all the nodes and for every node, check if we have already encountered this node. If we ecnounter a node which has already been visited before, then the linked list has a loop. We can efficiently check if the node has already been visited by maitaining a HashSet of already visited nodes. The starting node of the loop will the first repeated node encountered.

If the linked list does not have a loop, then the traversal of the list will terminate without encountering any repeated node.

Implementation

Complexity

In this method, we traverse through all the nodes only once except the first repeated node if it exists. The repeated node will be traversed twice. Checking for a repeated node using HashSet is a constant time operation. $\therefore$ The Time Complexity of this method is ${\cal O}(n)$ time.

But we are saving each traversed node into a HashSet. $\therefore$ The Space Complexity of this method is also ${\cal O}(n)$ time.

Solution 2: Efficient Solution (Floyd's Method)

Floyd gave a more efficient method than discussed above. This method is efficient in terms of the space used. Time Complexity remains ${\cal O}(n)$ while the Space Complexity is constant time ${\cal O}(1)$.

Principle

Floyd's method is based upon a principle that if two pointers - one moving at the speed of one node at a time and another at twice the speed of the first, are circulating in a loop, then they will always meet at a node.

At any time, if Faster Pointer is just behind the Slower Pointer, then in the next step, they will meet.

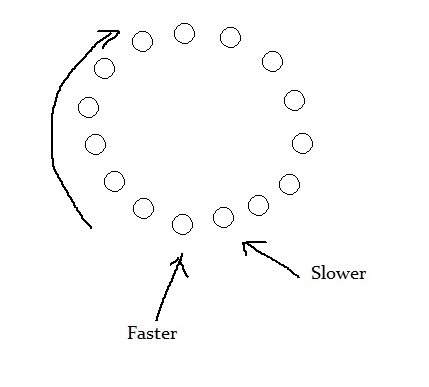
At any time, if the Faster Pointer is just aheadd of the Slower Pointer, this position is possible only if they have met in the previous step.

Detecting the Loop

Mathematics - Identify the Start of Loop

Let, when the two pointers intersect,

$\ \ \ \ \ \ m = length\ of\ the\ non-loop\ branch$
$\ \ \ \ \ \ n = length\ of\ the\ loop$
$\ \ \ \ \ \ k = length\ from\ starting\ point\ of\ the\ loop\ to\ the\ point\ of\ intersection$

$\ \ \ \ \ \ x = number\ of\ complete\ loops\ made\ by\ the\ slower\ pointer$
$\ \ \ \ \ \ y = number\ of\ complete\ loops\ made\ by\ the\ faster\ pointer$

Now,
$\ \ \ \ \ \ distance\ traveled\ by\ faster\ pointer\ (F) = m + k + yn$
$\ \ \ \ \ \ distance\ traveled\ by\ slower\ pointer\ (S) = m + k + xn$

Since, faster pointer has moving at double the speed of slower pointer,
$\ \ \ \ \ \ \ \ \ F = 2S$
$\ \ \ \ \ \ => m + k + yn = 2(m + k + xn)$
$\ \ \ \ \ \ => m + k + yn = 2(m + k) + 2xn$
$\ \ \ \ \ \ => m + k = yn - 2xn$
$\ \ \ \ \ \ => m + k = n(y - 2x)$
$\ \ \ \ \ \ => \because faster\ pointer\ is\ moving\ at\ double\ speed,\ (y - 2x) >= 1\ and\ is\ ALWAYS\ an\ Integer.$
$\ \ \ \ \ \ => m + k = certain\ number\ of\ COMPLETE\ loop\ cycles$

So, we can conclude that,

1. If Two Pointers (move at the same speed) start moving at the same time, one start from beginning of the linked list and another start from beginning of the loop, by the time the first Pointer travels $m + k$ nodes, the second Pointer will make certain number of complete loop and reach the beginning the loop again.
2. If the first pointer moves only $m$ nodes, then the second pointer will complete some loop and travel $n- k$ nodes.
3. If the second pointer starts from the point of intersection instead of beginning of the loop, both of the pointer will meet at the beginning of the loop. This is our REQUIRED start of the loop.

Compute Start of the Loop

So based upon the theory above, we can find the start of the loop by following way:

1. When the two pointers meet (the loop is detected), keep one pointer at the same location and move the other to the beginning of the linked list.
2. Now move the two pointers at the same speed - one node at a time.
3. When the two pointers meet, the meeting point will be the beginning of the loop.

Complete Implementation

Time Complexity

Time complexity is ${\cal O}(n)$ and the Space complexity is ${\cal O}(1)$.

---

---

---